Signification du volume d'une sphère
Pour visualiser une sphère, considère tous les cercles congruents possibles dans l'espace qui ont le même point pour centre. Ensemble, ces cercles forment une sphère. Tous les points de la surface de la sphère sont à égale distance de son centre. Cette distance est le rayon de la sphère.
Dans l'espace, une sphère est le lieu de tous les points qui se trouvent à une distance donnée d'un point donné - son centre.
L'espace total occupé par une sphère est appelé le volume de la sphère.
Formule du volume d'une sphère
La formule pour calculer le volume V d'une sphère de rayon r est la suivante
![]()
Pourquoi utilisons-nous cette formule pour calculer le volume d'une sphère ? Tu peux établir un lien entre la formule du volume d'une sphère, le volume d'une pyramide droite et la surface de la sphère.
Suppose que l'espace à l'intérieur d'une sphère soit séparé en une infinité de quasi-pyramides, dont les sommets sont tous situés au centre de la sphère, comme indiqué ci-dessous :
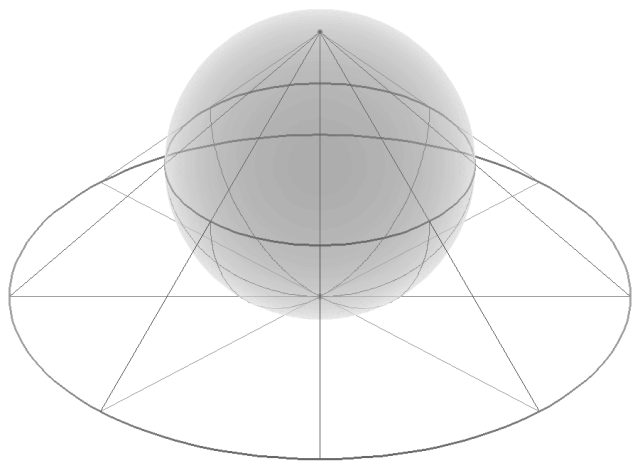
Fig. 1 : La sphère en tant que combinaison d'une infinité de quasi-pyramides
La hauteur de ces pyramides est égale au rayon r de la sphère. La somme des surfaces de toutes les bases des pyramides est égale à la surface de la sphère.Chaque pyramide a un volume de ![]()
, où B est la surface de la base de la pyramide et h sa hauteur. Le volume de la sphère est donc égal à la somme des volumes de toutes les petites pyramides.
![]()
Volume d'une sphère de diamètre
Suppose qu'au lieu du rayon, on te donne le diamètre de la sphère. Puisque le diamètre est le double du rayon, nous pouvons simplement substituer la valeur ![]()
dans la formule ci-dessus. Ce qui donne :
![]()
Volume d'une sphère Calculs avec exemples
Examinons quelques calculs liés au volume des sphères.
Volume d'une sphère Exemples
Nous allons examiner plusieurs exemples pour donner une bonne explication sur ce sujet.
Trouve le volume d'une sphère de rayon 4.
Solution
![]()
On parle de grand cercle lorsqu'un plan coupe une sphère de façon à ce qu'il contienne le centre de la sphère. En effet, un grand cercle est un cercle contenu dans la sphère dont le rayon est égal au rayon de la sphère. Un grand cercle sépare une sphère en deux moitiés congruentes, chacune appelée hémisphère.
Trouve le volume d'une sphère dont le grand cercle a une aire de 154 unités2.
Solution
Aire du grand cercle ![]()
![]()
![]()
Le volume d'une sphère est de ![]()
. Trouve le rayon de la sphère.
Solution
![]()
Le volume d'une sphère est de ![]()
. Trouve le diamètre de la sphère.
Solution
![]()
Trouve le volume d'une sphère ayant un diamètre de 2 unités.
Solution
![]()
Volume des sphères - Principaux enseignements
- Dans l'espace, une sphère est le lieu de tous les points qui se trouvent à une distance donnée d'un point donné appelé son centre.
- Le volume V d'une sphère de rayon r est donné par la formule :
![]()
- Le volume V d'une sphère dont le diamètre est d est donné par la formule :
![]()
Resumes 
Flashcards 
StudySmarter IA 
Notes de cours 
Planning de révision 
Dossiers 
Examens 
Magazine 
Faire carrière 
App mobile 
