Qu'est-ce que la formule de la somme et de la différence des angles en trigonométrie ?
Contrairement aux opérations arithmétiques normales, l'addition et la soustraction des fonctions trigonométriques ont une approche différente. Par exemple, cos (45° -15°) n'est pas la même chose que cos45° - cos15°. Cela devient plus difficile lorsque des fonctions trigonométriques sont impliquées dans de telles opérations arithmétiques. Il faut donc trouver des formules pour résoudre ce problème.
Connaître les fonctions trigonométriques des angles spéciaux tels que les sinus, les cosinus et les tangentes de 30, 45, 60 et 90 degrés signifie que l'addition ou la soustraction de ces angles peut donner d'autres angles. Par exemple, sin15° peut être dérivé, puisque sin15° est identique à sin(45-30)° . Par la suite, nous déduirons des formules pour résoudre ces opérations.
Différence des fonctions cosinus
Considère la figure ci-dessous :
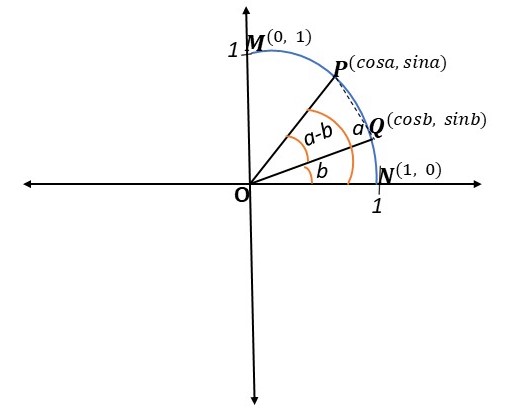
Figure 1 : Une image montrant l'utilisation de la position standard d'un cercle unitaire pour prouver la différence des fonctions cosinus, - StudySmarter Originals
La figure ci-dessus est prise dans la position standard d'un cercle unitaire. Si a est l'angle ∠PON et b l'angle ∠QON, alors l'angle ∠POQ est (a - b) . Par conséquent , est la composante horizontale du point P etest sa composante verticale. Tandis queest la composante horizontale du point Q et est sa composante verticale. Ainsi, pour trouver la distance PQ, nous utiliserons la formule de la distance entre deux points.
Où dans le point P, est et au point Q, est. Ainsi, le point P est et le point Q est .
Réarrange l'équation
Rappelle-toi :
Ensuite :
Si l'angle ( a-b) était replacé dans la position standard d'un cercle unitaire allant de l'origine O au point S dans la figure ci-dessous
 Figure 2 : Une image de l'angle (a-b) en train d'être retracé, - StudySmarter Originals
Figure 2 : Une image de l'angle (a-b) en train d'être retracé, - StudySmarter Originals
Ensuite, la distance SN de la figure 2 (qui est égale à la distance PQ de la figure 1) peut être dérivée par rapport à l'angle ( a-b) et aux points correspondants dans S (cos (a-b), sin(a-b) ) et N (1 , 0).
Utilisation
Où le point S est et N est alors
Réarrange et rapproche les termes similaires
Rappelle-toi que
alors ;
Rappelle-toi que
alors
Ainsi
Résous l'algèbre en soustrayant 2 des deux côtés de l'équation.
Divise les deux côtés par -2 des deux côtés
Somme des fonctions cosinus
Ainsi, remplace la valeur de b par -b dans l'équation.
Note que
et
donc
Somme des fonctions sinusoïdales
Dessine un triangle rectangle ABC comme indiqué ci-dessous.
 Une image d'un triangle droit, - StudySmarter Originals
Une image d'un triangle droit, - StudySmarter Originals
Trace une autre ligne coupant A et touchant la ligne BC en D, de telle sorte que l'angle BAD soit β et l'angle DAC soit α, comme on le voit ci-dessous.
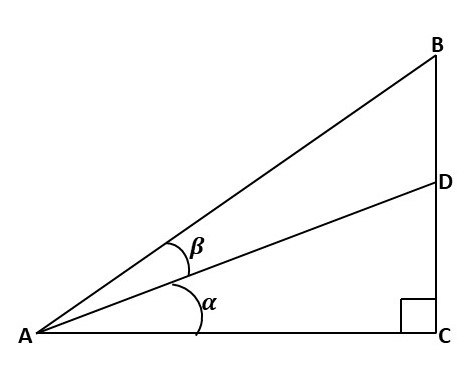
Trace une ligne perpendiculaire au point D qui touche la ligne AB en E comme indiqué ci-dessous.
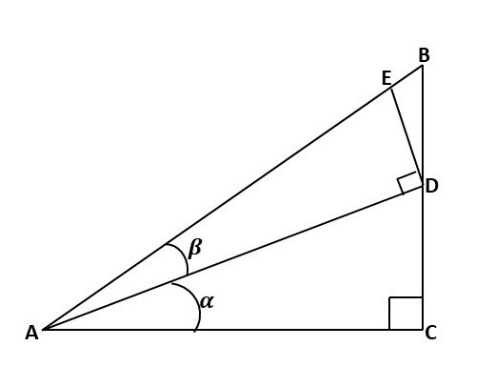
Trace une ligne à partir du point E qui est perpendiculaire à la ligne AC, coupe la ligne AD en F et rencontre la ligne AC en G comme indiqué ci-dessous.
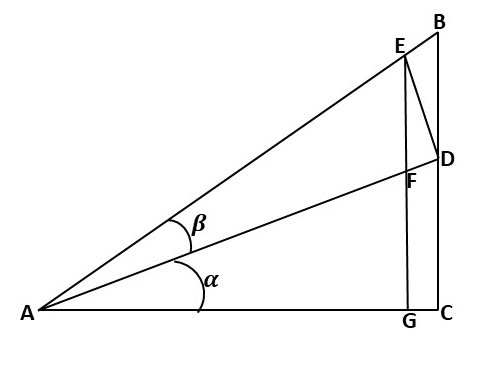
Trace une ligne allant du point D au point H sur la ligne EG qui est perpendiculaire à la ligne EG comme indiqué ci-dessous.
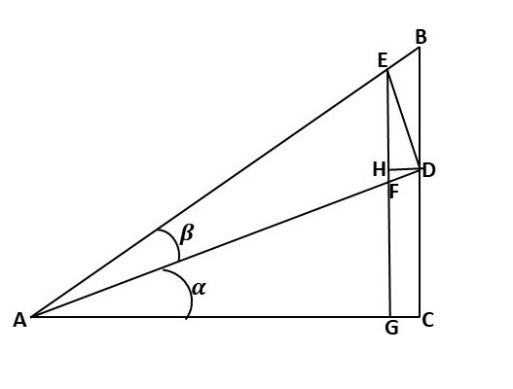
Note que pour chaque étape ci-après, tu dois te référer à la figure ci-dessus.
Par conséquent
Utilisation de SOHCAHTOA
Note que la ligne EG = EH + HG, donc
Rappelle ;
les droites HG et DC sont parallèles et égales.
Ainsi
Vois que
Ce sont des angles alternés car les lignes HD et AC sont parallèles et sont coupées par la ligne AD.
Note ci-dessous
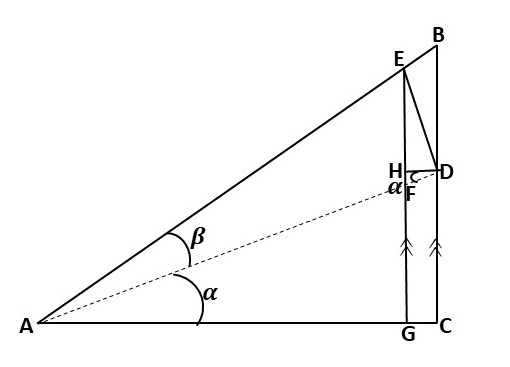
Rappelle-toi que la ligne AD est perpendiculaire à la ligne ED. Par conséquent
Sachant que
donc
La somme des angles d'un triangle est égale à 180°.
En regardant leurs angles, cela signifie que les triangles ADC et EDH sont similaires. voir ci-dessous
 Une image qui prouve la somme des sinus des angles, StudySmarter Originals
Une image qui prouve la somme des sinus des angles, StudySmarter Originals
À partir du triangle rectangle EDH
Rappelle-toi que
Substitue la valeur de EH
En attendant, à partir du triangle rectangle AED, en utilisant SOHCAHTOA
Substitue la valeur de dans l'équation
A partir du triangle rectangle ADC, à l'aide de SOHCAHTOA
Substitue la valeur de DC dans l'équation
Regarde le triangle rectangle AED et utilise SOHCAHTOA
Substitue la valeur de dans l'équation
Différence de ses fonctions
Sachant que
Ainsi peut être dérivé en échangeant β avec -β tout au long de l'équation.
Par conséquent
Note que
et
donc
Somme des fonctions tangentes
Rappelle-toi que
Par conséquent
Par conséquent
Divise chaque entité du côté droit de l'équation par cosAcosB
Différence des fonctions tangentes
Rappelle-toi que
Par conséquent
Ainsi
Divise chaque entité du côté droit de l'équation par cosAcosB
Application de la somme et de la différence des formules
Tu verras ci-dessous comment appliquer les formules de somme et de différence.
Trouve la valeur de cos15°
Solution :
La première étape consiste à trouver la meilleure combinaison possible d'angles spéciaux qui donnera cet angle. Dans ce cas, on obtient 15° en soustrayant 30° de 45°.
Par conséquent
rappelle
Par conséquent ;
Factorise davantage
id="5217730" role="math"
Donc
id="5217731" role="math"
Prouve que :
Solution :
sachant que
Par conséquent
Note que
:
Ainsi ,
D'où ;
Si un homme quitte un point P pour se rendre à un point R situé à 20 km à l'est de P, il marche ensuite jusqu'à un point S situé au nord de R. Trouve la distance entre R et S si S est à 75 degrés au nord-est de P sans utiliser de calculatrice ou de table mathématique.
Solution :
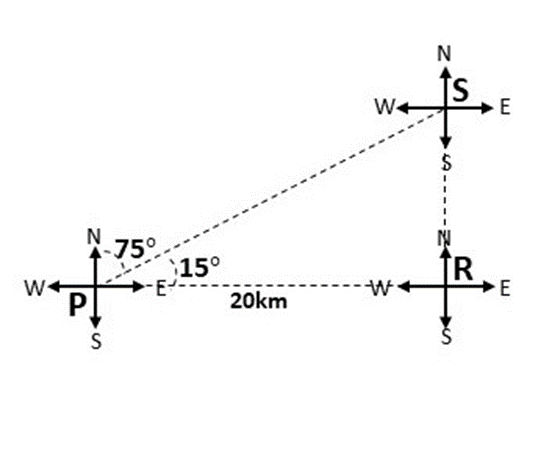
On nous demande de calculer la distance RS. Utilisation de SOHCAHTOA
Note que
Par conséquent
Où
et
Alors
Multiplie le numérateur et le dénominateur par
Par conséquent
Formules de la somme et de la différence des angles - Principaux enseignements
- La somme et la différence des fonctions trigonométriques ne se calculent pas en utilisant une approche arithmétique directe.
- La formule de la somme et de la différence du sinus est la suivante
- La formule de la somme et de la différence du cosinus est la suivante
- La formule de la somme et de la différence de la tangente est la suivante

















