Les identités trigonométriques sont importantes pour résoudre toute une série de problèmes et d'équations avancées. Elles nous permettent de simplifier de nombreux problèmes et de rendre les situations plus faciles.
Merci de votre intérêt pour les préférences d’apprentissage !
Merci pour ton intérêt pour les différentes méthodes d’apprentissage ! Quelle méthode préfères-tu ? (par exemple, « Audio », « Vidéo », « Texte », « Pas de préférence »)
(optionnel)
Traçons tout d'abord un triangle dont l'angle est θ.
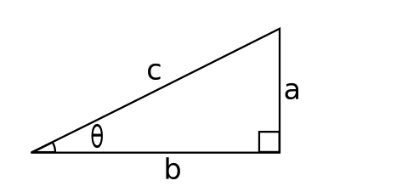
Triangle général d'angle θ
Maintenant, si nous écrivons les expressions pour a et b en utilisant SOHCAHTOA, nous obtenons :
Par conséquent :
Maintenant, si nous élevons au carré ces deux expressions pour sin et cos, nous obtenons :
En les additionnant, on obtient :
Par le théorème de Pythagore :
Par conséquent :
Passons maintenant à la preuve . La première moitié de cette preuve est identique à la preuve ci-dessus.
PREUVE :
Traçons tout d'abord un triangle dont l'angle est θ.
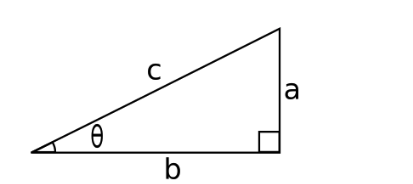
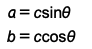
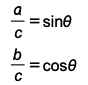
Maintenant, si nous écrivons les expressions pour a et b en utilisant SOHCAHTOA, nous obtenons :Donc Maintenant, si nous divisons ces deux expressions pour sin et cos :
Il s'agit d'une expression pour le côté opposé sur le côté adjacent, donc :
Donc :
Voyons maintenant quelques exemples pratiques où les identités trigonométriques peuvent être appliquées.
Exemples d'exercices utilisant les identités trigonométriques
Résous l'équation pour
SOLUTION :La première chose à faire est de substituerpar .L'équation est maintenant la suivante .En simplifiant davantage :Nous pouvons maintenant résoudre cette équation comme une quadratique en prenant .Nous devons maintenant faire x = cos-1(y)Nous ne pouvons faire que cos-1(0,5)=60°C'est parce que 1,5 > 1 et que nous ne pouvons donc pas faire une fonction cos-1 de ceci.La seule réponse est donc 60°.
Voyons un autre exemple de réarrangement des identités trigonométriques.
Montre que l'équation peut s'écrire sous la forme
SOLUTION :Tout d'abord, réarrangeons l'équation pour éliminer les dénominateurs.Remplaçons maintenant par :Maintenant, débarrasse-toi du dénominateur en multipliant par :Remplaçons maintenant par :Réarrange ensuite cette équation :QED
Quelles autres identités trigonométriques pouvons-nous déduire ?
Tout d'abord, nous devons connaître trois nouveaux éléments de terminologie :
Il s'agit des réciproques des sin, cos et tan standard.
Dériver de nouvelles identités
Examinons maintenant l'identité :
Si nous divisons l'équation entière par nous obtenons :En utilisant l'identité :C'est notre première nouvelle identité. Maintenant, si nous divisons toute notre équation par En utilisant l'identité , donc :Nous avons maintenant nos deux nouvelles identités :
Voyons-les en action dans quelques exemples concrets.
Exemples travaillés de nouvelles identités
Résous, pour 0 ≤ θ < 360°, l'équation :
à 1 dp.
Graphique de y=cosx. Image : Ruben Verhaegh, CC BY-SA 4.0
Nous pouvons voir que si nous effectuons l'identité l'autre valeur de est .
Nous devons alors effectuer en utilisant à nouveau l'identité , .
Ainsi, à 1 décimale près, nos 4 solutions en degrés sont :
Apprends plus vite avec les 1 fiches sur Identités trigonométriques
Inscris-toi gratuitement pour accéder à toutes nos fiches.
Questions fréquemment posées en Identités trigonométriques
Qu'est-ce qu'une identité trigonométrique?
Une identité trigonométrique est une équation valable pour toutes les valeurs des angles impliqués. Exemple : sin²(θ) + cos²(θ) = 1.
Pourquoi utilise-t-on les identités trigonométriques?
On utilise les identités trigonométriques pour simplifier les expressions trigonométriques, résoudre des équations et comprendre les relations entre les fonctions trigonométriques.
Quelle est l'identité trigonométrique fondamentale?
L'identité trigonométrique fondamentale est : sin²(θ) + cos²(θ) = 1. Elle exprime la relation entre le sinus et le cosinus d'un angle.
Comment prouver une identité trigonométrique?
Pour prouver une identité trigonométrique, on manipule les expressions avec des transformations algébriques et l'utilisation d'autres identités jusqu'à ce que les deux côtés de l'équation soient égaux.
Comment tu t'assures que ton contenu est précis et digne de confiance ?
Chez StudySmarter, tu as créé une plateforme d'apprentissage qui sert des millions d'étudiants. Rencontre les personnes qui travaillent dur pour fournir un contenu basé sur des faits et pour veiller à ce qu'il soit vérifié.
Processus de création de contenu :
Lily Hulatt
Spécialiste du contenu numérique
Lily Hulatt est une spécialiste du contenu numérique avec plus de trois ans d’expérience en stratégie de contenu et en conception de programmes. Elle a obtenu son doctorat en littérature anglaise à l’Université de Durham en 2022, a enseigné au Département d’études anglaises de l’Université de Durham, et a contribué à plusieurs publications. Lily se spécialise en littérature anglaise, langue anglaise, histoire et philosophie.
Gabriel Freitas est un ingénieur en intelligence artificielle possédant une solide expérience en développement logiciel, en algorithmes d’apprentissage automatique et en IA générative, notamment dans les applications des grands modèles de langage (LLM). Diplômé en génie électrique de l’Université de São Paulo, il poursuit actuellement une maîtrise en génie informatique à l’Université de Campinas, avec une spécialisation en apprentissage automatique. Gabriel a un solide bagage en ingénierie logicielle et a travaillé sur des projets impliquant la vision par ordinateur, l’IA embarquée et les applications LLM.
StudySmarter est une entreprise de technologie éducative mondialement reconnue, offrant une plateforme d'apprentissage holistique conçue pour les étudiants de tous âges et de tous niveaux éducatifs. Notre plateforme fournit un soutien à l'apprentissage pour une large gamme de sujets, y compris les STEM, les sciences sociales et les langues, et aide également les étudiants à réussir divers tests et examens dans le monde entier, tels que le GCSE, le A Level, le SAT, l'ACT, l'Abitur, et plus encore. Nous proposons une bibliothèque étendue de matériels d'apprentissage, y compris des flashcards interactives, des solutions de manuels scolaires complètes et des explications détaillées. La technologie de pointe et les outils que nous fournissons aident les étudiants à créer leurs propres matériels d'apprentissage. Le contenu de StudySmarter est non seulement vérifié par des experts, mais également régulièrement mis à jour pour garantir l'exactitude et la pertinence.
Resumes 
Flashcards 
StudySmarter IA 
Notes de cours 
Planning de révision 
Dossiers 
Examens 
Magazine 
Faire carrière 
App mobile 
et 
Maintenant, si nous écrivons les expressions pour a et b en utilisant SOHCAHTOA, nous obtenons :
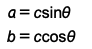Donc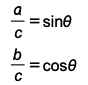 
Maintenant, si nous divisons ces deux expressions pour sin et cos :
